So you’ve been tasked with the less illustrious side of performance analysis, finding out how far your plane can actually fly using a given amount of fuel. Or maybe you’re tasked with finding out how much fuel the aircraft needs to perform a mission. Seems easy right? Well there are a lot of things that go into this that make it hard. The primary being that range is path dependent, you have less range if you constantly dive and climb, if you have to do any maneuvers, and when and where you drop cargo if you have it. This post should help give you a solid starting place assuming you have a good background in some basic engineering analysis and terms.
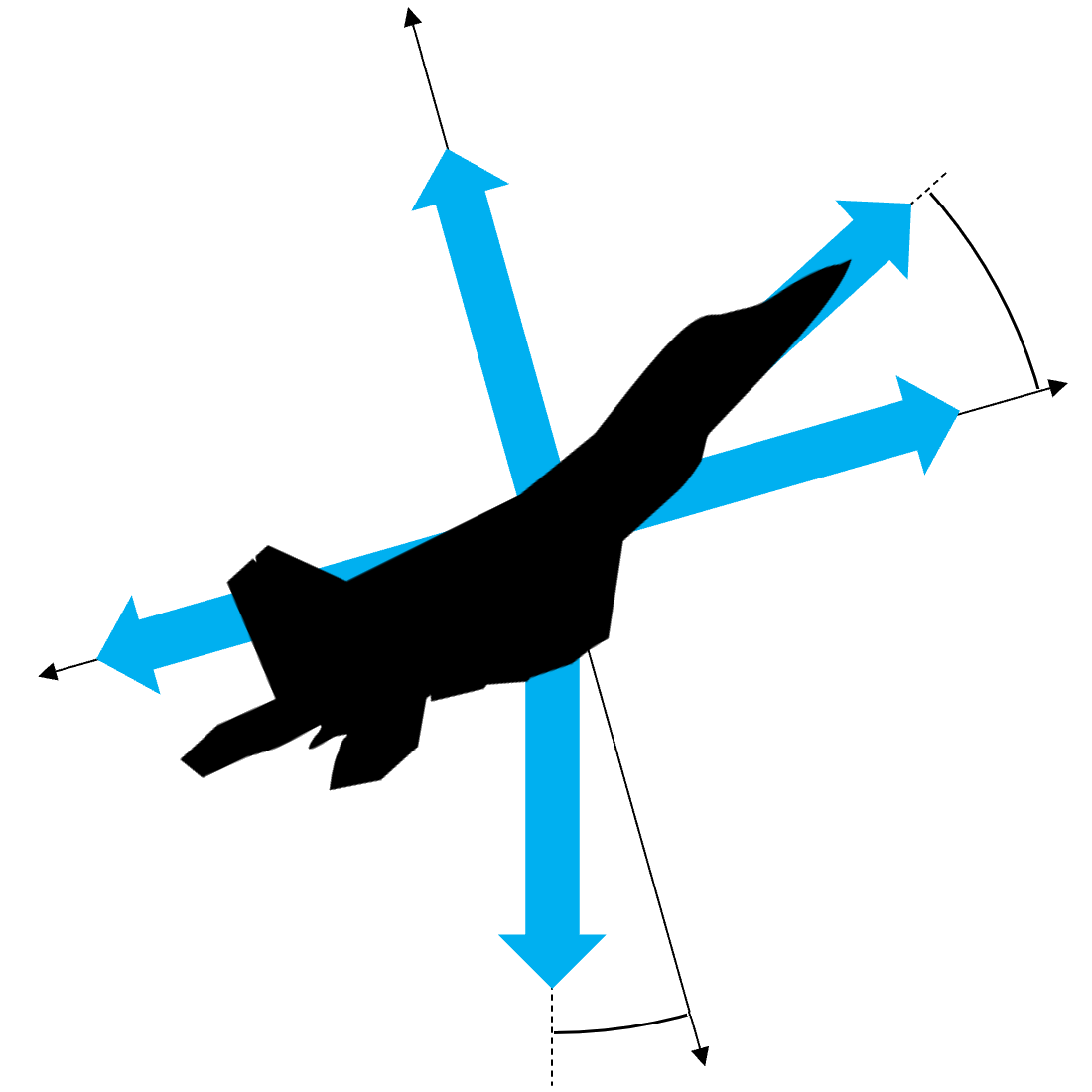
The first step to solving this problem is by isolating all of the forces acting on the aircraft. And already we have to make our first engineering assumptions. Since turning typically takes up a small portion of a typical fixed wing flight path I model the aircraft traveling in one plane, with all forces acting in that same plane. Additionally I assume that all of the forces act at the center of mass meaning that the resultant moments are all zero which is valid depending on how you performed your aerodynamic analysis (Did you already account for the control surface deflection needed to maintain cruise? Did you include the variable control surface drag in your whole vehicle drag analysis?). This diagram importantly does not assume that the thrust always acts along the path which is very important for heavy aircraft flying slowly.

For the above free body diagram the forces considered are:
- Lift
- Drag
- Thrust
- Weight
Additionally there are two important angles described:
- The angle of attack α, which changes how much lift and subsequently drag is produced.
- The flight path angle θ, which is the angle the path the aircraft is flying to the horizon. Positive values mean that the aircraft is climbing, negative angles mean that the aircraft is descending, and when set to zero means that the aircraft is maintaining altitude.
Solving the force balance gives us two equations for the resultant forces on the craft:

Force Balance Analysis
In order to model the aircraft all of the variables that effect the forces acting on the aircraft must be accounted for. Of those variables there are two categories. The first being variables that dynamically change in flight and and second are variables that are set by vehicle design.
| Force from Free Body Diagram: | Flight Variables: | Vehicle Properties: |
|---|---|---|
| Lift | Free stream velocity, Mach number, density, angle of attack | Aspect ratio, sweep, airfoil section, planform area |
| Drag | Free stream velocity, Mach number, lift coefficient, density, angle of attack | Planform area, 0 lift drag coefficient |
| Thrust | Density, throttle setting | Engine choice |
| Weight | Sum of all fuel burned, path angle | Materials, weight of structures, etc |
Once we have general idea of the variables that effect each force we have to chose how to model the forces and whether or not the variables we listed need to be included in the analysis. There are a LOT of different approaches that can be taken here, here are a few that I considered for my project with a few of the main limitations mentioned:
| Aerodynamic Modeling Approaches |
|---|
| Model the aircraft in OpenVSP or XFlr5 and use their built in vertex lattice methods to solve for whole vehicle aerodynamic loads/coefficients if you’re operating at low enough Reynold’s numbers. (This is the easiest option with the most “bang for your buck” but you have to be careful of the assumptions that are used in the solvers and each programs’ general limitations.) |
| Use OpenVsp to generate various vehicle meshes for various control surface defection and run all of those through CFD at various altitudes, configurations, and flight stages. (this requires extensive aerodynamic experience in most cases, most companies wont have analysts perform CFD without at least an MS in the field) |
| Use empirical relationships outlined in exhaustive detail in this textbook. |
Creating Fuel Efficiency Curves
Now that you have a model for three of the forces from the free body diagram it is possible to solve for the thrust required and angle of attack simultaneously if you set the sum of all forces to zero in our case for steady state flight. However that alone doesn’t tell us everything that we need to know. The Thrust Specific Fuel Consumption, TSFC (typically in lbflbm-1hour-1), of most engines is readily available at take off power settings but it can be very difficult to find accurate flight data with differing flight conditions. Mach number, thrust, and density can change the TSFC of any engine dramatically. Even worse, all of those relationships change between turboprops, piston driven props, turbojets, and low and high bypass ratio turbofans. A good place to start with high bypass ratio turbofans is here and they go into good detail. The relationship that I ended up using to calculate instantaneous burn rate ended up being a function of thrust, Mach number, and altitude.

Finally using the solved thrust and the new relationship for thrust specific fuel consumption the fuel consumption in lb/nmi is found by using the equation below.

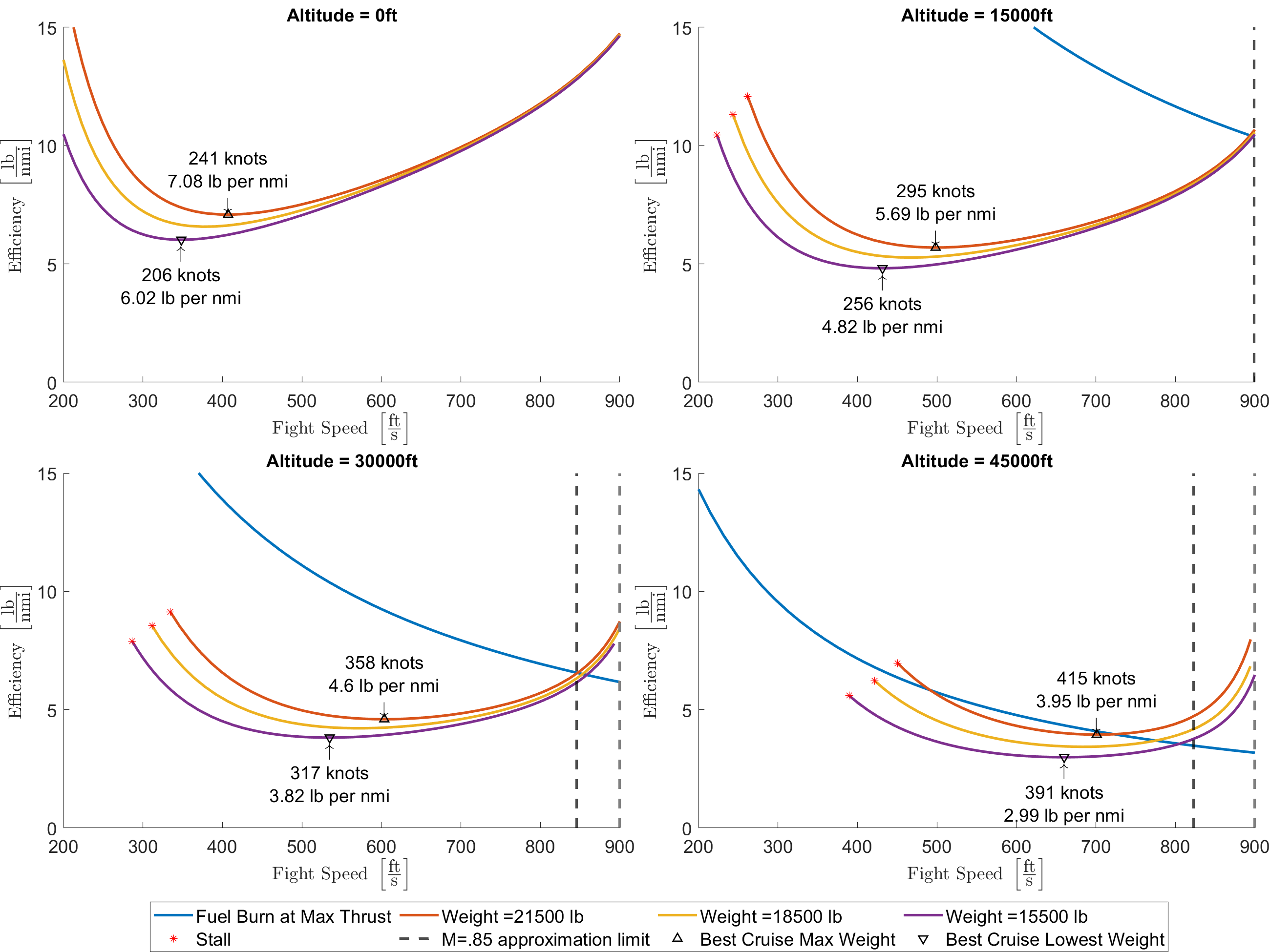
Plotting the consumption with various aircraft weights and flight speeds yields the graph to the left, which is very handy to know instantaneous consumption at fixed altitudes but makes finding the best cruising altitude and speed combination dubious. All of these values represent level flight for a single-engine aircraft and all altitudes are relative to sea level.

In order to find the best cruising altitude and speed for the lowest consumption per mile (best range) the same calculations are done but this time the altitude and flight speed are used as independent variables with the consumption being represented in these 3d pork chop plots.
Its important to take a step back here and make sure that what these graphs are showing you makes sense physically. Does it make sense that a lighter aircraft can fly at a higher altitude using less fuel? These graphs along with any contract requirements or airspace restrictions are instrumental in designing a simple and efficient mission profile as described in the next section.

The last graphs were instrumental in finding the lowest possible fuel consumption per nautical mile but loitering at those speeds would be incredibly wasteful. In order to calculate the best loiter conditions the power must be taken into account.

This graph gives a general trend of how loitering favors a lighter aircraft traveling slower but doesn’t give us a good way to optimize loitering or an instantaneous fuel burn.

Just like the last pork chop plot the altitude and flight speed are used as independent variables with the power required represented as the third dimension.
Again, its very important to take a step back and make sure that what this graph is showing you makes sense physically. Does it make sense that optimizing loiter fuel burn requires slow flight at low altitudes?
Choosing and Describing a Mission Path
One of the most important steps of calculating the aircraft fuel consumption is describing the path that your aircraft will take. In fact all of the graphs created before used a set mission path with a zero degree flight path angle to represent level flight. In addition to describing the path it must actually be physically possible. There are a lot of important considerations required but a few simple shortcuts can be taken to find most physically impossible flight conditions in a profile.
| Simple Checks |
|---|
| Is the angle of attack less than ~10 degrees? (VERY important while using VSPAero or XFLIR-5, by default these do not properly model lift at high angles of attack) For very rapid ascents and take-offs this question should be changed to “Is the calculated lift possible given my aircraft configuration?” |
| Is the thrust required higher than the maximum thrust for the assumed flight state? |
| Is the thrust required below the minimum thrust the engine can sustain at this flight state? |
For my aircraft a significant portion of the path was predetermined by contract requirements and two separately laid out missions. The flight path has to describe free stream velocity, altitude, and the path angle for every point on the mission path. I plotted mine below versus mission time.

And now that we have a mission path we can verify that it is flyable by checking that the angle of attack stays lower than about 10 degrees and that the “throttle” (current thrust/max thrust at flight state) stays below 100% and above 10%.

Calculating Fuel Burn
Finally we have everything we need to calculate fuel burn, with another assumption of course, one made in the last section. The flight path described in the previous section assumes instantaneous transitions between flight stages. Getting the fuel consumption is hard because it depends on the fuel consumption, does that make sense? The weight of the aircraft changes the burn rate and the burn rate changes the weight of the aircraft so at first glance this seems like a circular problem, except for the fact that the starting weight can be assumed to be GTOW or otherwise assigned. The easiest way to solve this is with numerical integration, and the easiest (and worst) way to numerically integrate is using Euler’s method. I used the mission path to find the velocity, flight path angle, and altitude at every second of the flight and used those values to calculate the burn-rate.
t = 0 %starting time
delta = 1 %time step
w = GTOW %starting weight
while t < missionTime
[θ,v,h] = missionPath(t)
mdot = bRate(thrust(α(w,v,h,θ)),v,h)
w = w - mdot*delta
t = t + delta %increment by delta
end
disp("Fuel burned: ",(GTOW - w)) Of course this approach is far from perfect, and must be verified. If the resulting fuel burn is greater than the amount of fuel in the design than that means your pilot would be having an exceptionally bad time. That’s about everything that goes into this calculation if you want to generate pretty graphs like the one below than you would need to store the weight, thrust, and burn-rate at each iteration.

Aircraft Used in Figures
| General Properties | Values |
| Engine | Safran M88; Thrust Specific Fuel Consumption (TSFC) = 0.782 |
| Gross Take-off Weight | GTOW = 21,500 lbf |
| Whole Wetted Surface Area | Sw=1,260 ft2 |
| Wing Properties | Values |
| Planform Area | S=337 ft2 |
| Airfoil | Cl,α=0.11/deg; Cl,0=0.25 |
| Root Chord | cr=9.17 ft |
| Tip Chord | ct=6.17 ft |
| Span | b=44 ft |
| Aspect Ratio | AR = 5.74 |
| Mid Chord Sweep | Λc/2 = 10 degrees |